Tenho visto um monte de gente comprando a historinha esdrúxula de que “raiz quadrada” seria uma tradução errada de radix quadratum. Pros autores da “pérola”, radix quer dizer lado, não raiz. A ideia teria sua lógica, não fosse baseada em pressupostos falsos.
Radix em latim quer dizer base, fundamento, origem, raiz. É dela que derivam as palavras radical (relativo à raiz), radicar e arraigar (enraizar, criar raízes). Lado em latim é latus, de onde deriva a própria palavra lado, como também (através de lateralis) lateral e colateral.
A hipótese da tradução errada fica meio ridícula quando pensamos em outas línguas. Em inglês é square root, em espanhol, raíz cuadrada, em alemão, quadratwurzel, em italiano, radice quadrata, em árabe, جذر تربيعي, em japonês, 平方根.
OK, todas as línguas latinas podem ter tradutores burrões que fizeram a mesma bobagem, mas que desculpa se dá pras outras línguas, onde a tradução é “raiz”, também?
Mas que raiz é essa?
Bom, desfeita a confusão etimológica, vamos entender esse negócio.
Sabemos que um quadrado é uma figura geométrica com quatro lados iguais. Assim, para calcular a área de um quadrado, basta multiplicar um lado por ele mesmo. Mas se soubermos a área, como descobrir o valor do lado? Aí é que entra a tal da raiz quadrada.
Essa compreensão é bastante antiga, tendo registros escritos com quase 4 mil anos na Babilônia, Egito, Índia e outros. Tal teoria chegou ao ocidente através dos árabes. Para eles, um quadrado “cresceu” (como uma árvore) a partir de um número (seu lado). Daí “raiz”.
Assim, a raiz quadrada seria a “base” do quadrado, ou seja, o valor do qual derivaram todos os lados da figura.
E o símbolo √, de onde vem?
Não há um consenso sobre isso, com duas versões principais: uma de que o símbolo derivaria da letra ج, que é a primeira letra da palavra árabe جذر (raiz) e a outra de que seria uma adaptação da letra r, primeira letra da palavra latina radix. O que se sabe é que o primeiro uso conhecido do símbolo impresso foi em 1525, no livro Die Coss1, do matemático Christoph Rudolff. No livro, o símbolo √ era usado sem aquela linha sobre os números, que só foi introduzida um século depois.
O uso do símbolo √ só passou a ser comum no Século XVII. Antes disso, vários outros símbolos foram sendo usados, mas nenhum com aceitação generalizada.
No Século XIII, o matemático italiano Leonardo Bonacci, conhecido como Fibonacci, em seu livro Liber Abbaci, descrevia as operações por extenso. Então, √16 = 4 era descrito por ele como radix quadratum 16 aequalis 4.
No Século XV, o matemático alemão Johannes Müller von Königsberg, conhecido como Regiomontanus, propôs o uso de um R estilizado que juntava a primeira e a última letras de radix. Algo como:
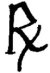
Em 1545 (20 anos após Rudolff, portanto), o polímata italiano Girolamo Cardano usava simplesmente uma letra R maiúscula em seu livro Artis Magnæ2.
Conclusão
Seja um amante da matemática ou da etimologia, sempre desconfie dessas explicações meio mágicas, principalmente essas que atribuem termos científicos à imbecilidade dos outros. Convenhamos.
Tem milhares de lendas sobre etimologia das palavras Internet afora que são absolutas bobagens. Um exemplo famoso é a insanidade de que forró vem de for all (para todos) e não de forrobodó (festa) ou aluno, que deixou de ter origem no latim alumnus (discípulo) pra virar um tal de a-luno, que significaria “sem luz” (oi????).
Dica quente: consulte o dicionário. Vários dicionários online, como o Michaelis e o Priberam citam a origem da palavra. Tem também sites dedicados ao assunto, como Origem da Palavra ou Sua Língua.
Notas
- Behend und hübsch Rechnung durch die kunstreichen regeln Algebre so gemeinicklich die Coss genent werden (Cálculo ágil e bonito através das regras astutas da álgebra [que] são tão comumente chamados de “coss”)
- Artis Magnæ, Sive de Regulis Algebraicis Liber Unus (livro número um sobre A Grande Arte, ou As Regras da Álgebra)

Bem, quando eu aprendi sobre isso era a base do quadrado e não o lado, achei estranho mas cada um conta este conto do seu jeito.
CurtirCurtido por 1 pessoa
é lado correto, porque qualquer um dos lados, lado do quadrado 9 = 3, então qualquer dos lados é 3, a base pode ter dupla interpretação tb…
CurtirCurtir
Então, Erique, não tem “correto” nesse caso. Nem lado nem base. A teoria etimológica da “má tradução” é falsa (e absurda).
CurtirCurtir
Olá! Gostei muito da sua explicação. Vc possui algum e-mail para entrar em contato? E também gostaria de saber se vc possui mais postagens aqui no site, se sim, poderia disponibilizar os links ou escrever os títulos?
CurtirCurtir
Oi, Vitor.
A não ser os artigos que constam fonte, todos os artigos aqui são escritos ou traduzidos por mim. O e-mail de contato do site é o meu e-mail.
CurtirCurtir
Se radix significa “base, fundamento, origem” e latus significado lado. Entao porque é radix quadratum 16 aequalis 4. E nao latus quadratum 16 aequalis 4. Nao tem fundamento nenhum seu texto amigo.
E a traducao dos outros paises é justamente o mesmo erro cometido pelos autores de lingua portuguesa que utilizaram muito provalmente algum livro em dado momento que radix foi traduzido para raiz, visto que nao só o portugues mas outras linguam derivam do latim.
Latim é uma lingua complexa, nao se faz uma simples traducao literal sem saber o contexto e significado envolvido.
É algo como voce pegar uma frase, expressão do português “A vida cobra” e traduzir “The life snake”…
CurtirCurtir
Oi, Marcos.
Cara, a resposta está no texto: “radix quadratum” = “raiz quadrada” e “latus quadratum” = “lado quadrado”. Qual a dúvida?
Você diz que todos os tradutores de todas as linguas do mundo estão errados e cometem um erro, mas você mesmo acaba de concordar com a tradução.
Sugiro que leia o texto novamente, desta vez até o fim, É uma boa ideia clicar nas hiperligações contidas no texto. Elas ajudam a esclarecer e muitas vezes explicitam a fonte da informação.
CurtirCurtir
Bom, no texto você diz que é bobagem dizer que foi traduzido errado, e radix quadratum é literalmente raiz quadrada (o que é uma raiz quadrada?). Temos que avisar o autor original que ele está errado em propor isso, pois radix quadratum não significa lado do quadrado que ele quer achar, e sim alterar para latus quadratum. Pressupor que a “raiz quadrada” que virá nos textos traduzidos deve ter muito mais significado físico/geométrico do que lado do quadrado é no mínimo curioso.
De outra forma também tenho do latim, radici, radicem, etc, o que traduzido errado tira todo o contexto.
Pegando sua interpretação temos:
Radix quadratum 9 aequalis 3
Radici quadratum 9 aequalis 3
Radicem quadratum 9 aequalis 3
Radix, radici e radicem simplesmente viram “raiz”?
A causa raiz de um problema é a mesma raiz de uma árvore?
No latim radix é uma sinonímia de latus, sendo mais correto referir-se a radix quadratum como lado do quadrado do que simplesmente chamar de raiz quadrada.
Uma tradução/interpretação errada feita mil vezes torna-se verdade, para qualquer língua
CurtirCurtir
Faz tempo que eu não faço nada por aqui… Nem lembro a última vez que respondi comentários. Vamos lá:
Não sei de onde as pessoas tiram que latim não tem declinações (aliás, e como tem…).
Bom, Marcos, radix, radici e radicem são sim “raiz”. São variações de caso. Veja:
Temos ainda radicis (ablativo), radice (genitivo) e, ainda, seus plurais: radices, radicibus, radices e radicum.
Tudo isso aí significa “raiz” ou “raízes”.
Não sei de que dicionário Klingon você tirou que latus é sinonímia de radix. Isso não é verdade. Não há qualquer caso em que uma palavra pode substituir a outra.
Lembre-se que radix, sendo raiz, não se refere só à parte subterrânea das plantas. Figurativamente, é usado para se referir à base, origem ou fundamento de alguma coisa. Assim, a “raiz quadrada” é a base do quadrado, ou seja, de onde o quadrado se origina.
Se você se interessa realmente pelo assunto (e não por memes de Internet), várias plataformas tem cursos de latim, como Duolingo ou Udemy.
CurtirCurtir